Line Distance, Coordinate Calculator
Straight Line:
x1:
x2:
y1:
y2:
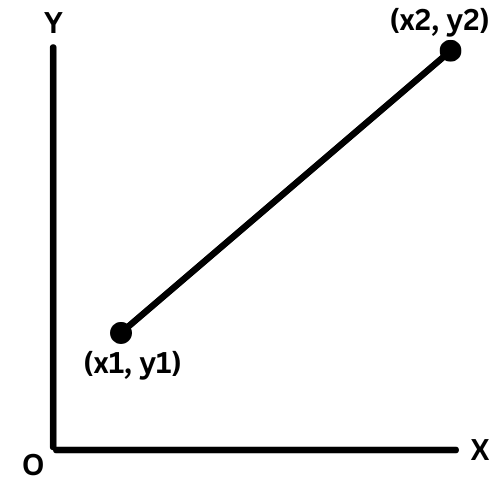Distance between two points:
√(x2 - x1)2+(y2 - y1)2
Example: What is the distance between two points (10,20) and (40,50)?
Answer: √ (40 - 10)2 + ( 50 - 20)2 = 42.426
Intermediate points (on the straight line):
x1:
x2:
y1:
y2:
r1:
r2:
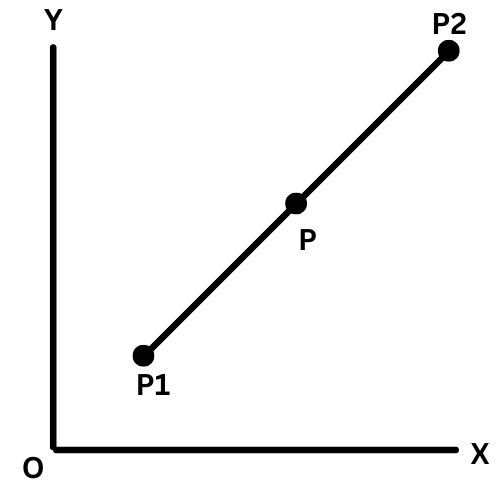Intermediate points (on the straight line):
x = (r1x1 + r2x2) / (r1 + r2)
y = (r1y1 + r2y2) / (r1 + r2)
Ratio of distance
r1: P1 to P to the distance of P1 to P2
r2: P2 to P to the distance of P1 to P2
Points P: (x,y), P1: (x1, y1), P2: (x2, y2)
Example: What is the coordinate of points (x,y), if (x,y) divides the straight line defined by points (1,2) and (20,45) at the ratio 4:2?
Answer:
x = (4*1 + 2*20) / (4+2) = 44/6 = 7.33
y = (4*2 + 2*45) / (4+2) = 98/6 = 16.33
External points (on the straight line and beyond):
x1:
x2:
y1:
y2:
r1:
r2:
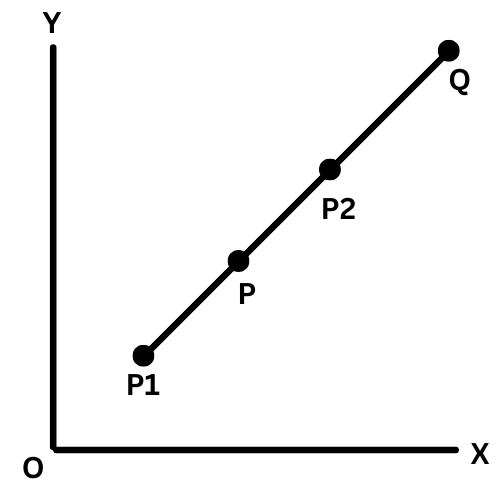External points (on the straight line and beyond):
x = (r1x1 - r2x2) / (r1 - r2)
y = (r1y1 - r2y2) / (r1 - r2)
Ratio of distance
r1: P1 to Q to the distance of P1 to P2
r2: P2 to Q to the distance of P1 to P2
Points Q: (x,y), P1: (x1, y1), P2: (x2, y2)
Example: What is the coordinate of points (x,y), if (x,y) are on the straight line and beyond defined by points (1,2) and (20,40) at the ratio 25:1?
Answer:
x = (25*1 - 1*20) / (25 - 1) = 5/24 = 0.21
y = (25*2 - 1*40) / (25 - 1) = 10/24 = 0.42
Parallel or Perpendicular Lines:
x1:
x2:
y1:
y2:
x3:
x4:
y3:
y4:
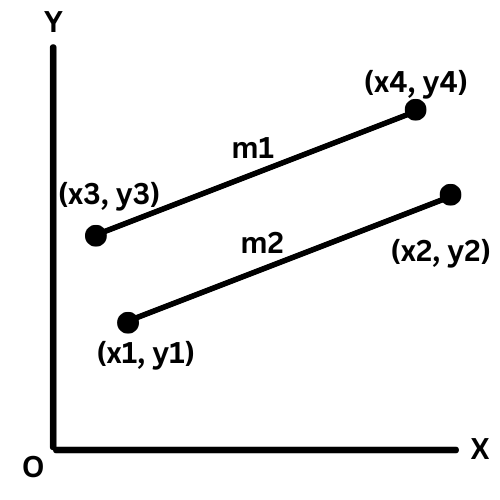
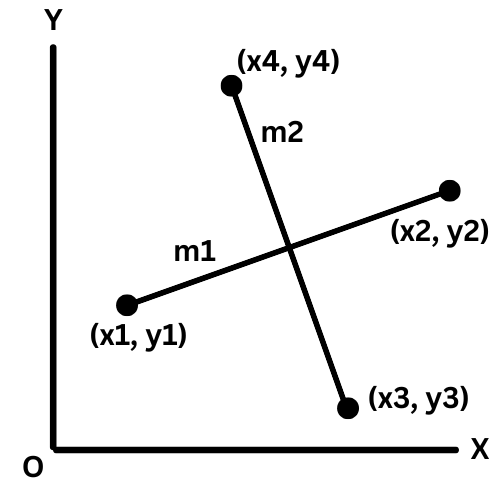Parallel or Perpendicular Lines:
m1 = (y2 - y1) / (x2 - x1)
m2 = (y4 - y3) / (x4 - x3)
Parallel Line: if (m1 = m2)
Perpendicular Line: if (m1m2 = -1)
Example: Line 1 has coordinates (1,3) and (4,6), Line 2 has coordinates (2,6) and (8,12). Find out if they are paralle or perpendicular?
Answer:
m1 = (6 - 3) / (4 - 1) = 3/3 = 1,
m2 = (12 - 6) / (8 - 2) = 6/6 = 1
m1 = m2 (Parallel Line)
Distance b/w point and line:
x:
y:
A:
B:
C:
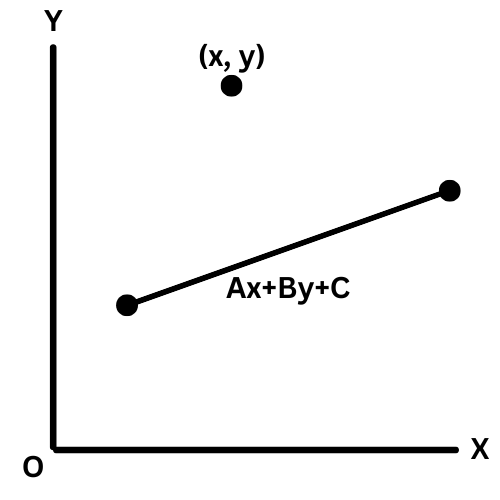Distance b/w point and line:
d = |A*x + B*y + C| / √ (A2 + B2)
Points P: (x,y)
Line: Ax + By + C
Example: Find the distance between the point (5,7) and line 2x + 3y - 8 = 0?
Answer:
d = |2*5 + 3*7 - 8| / √ (22 + 32) = 23 / √ 13 = 6.38