Functions of angles Calculator
Sides of a triangle:
a:
b:
c:
Angles of a triangle (°):
A:
B:
C:
(Enter either "3 sides" or "2 sides and 1 angle" or "1 side and 2 angles" above)
a / SinA = b / SinB = c / SinC
a = bSinA / SinB or a = cSinA / SinC
b = aSinB / SinA or b = cSinB / SinC
c = aSinC / SinA or c = bSinC / SinB
a2 = b2 + c2 - 2bcCosA
b2 = a2 + c2 - 2acCosB
c2 = a2 + b2 - 2abCosC
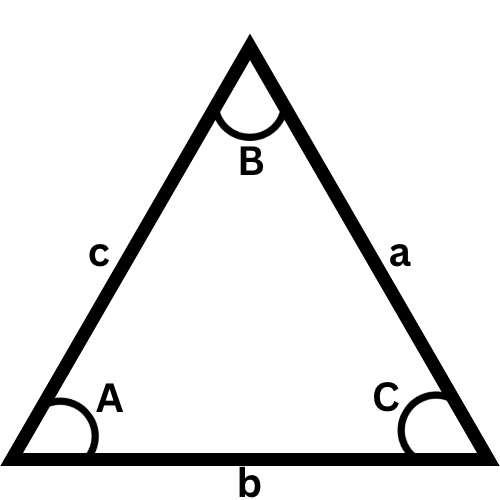
Example: If a is 1, A is 20° and B is 45° then find b, c, and C.
Answer: b = aSinB / SinA
b = 1*Sin45 / Sin20
b = 0.7071 / 0.342 = 2.067
C = 180 - (A + B)
C = 180 - (20 + 45) = 115
c = aSinC / SinA
c = 1*Sin115 / Sin20
c = 1*0.906 / 0.342 = 2.650
b = 2.067,
c = 2.65,
C = 115°
If A = 90°
Sides of a triangle:
a:
b:
c:
Angles of a triangle (°):
A: 90°
B:
C:
(Enter either "2 sides" or "1 side and 1 angle" above)
If a & b; c = √a2 - b2; SinB = b / a; C = 90 - B
If b & c; a = √b2 + c2; tanC = c / b; B = 90 - C
If a & c; b = √a2 - c2; SinC = c / a; B = 90 - C
If a & ∠B b = aSinB; c = aCosB C = 90 - B
If a & ∠C b = aCosC; c = aSinC B = 90 - C
If b & ∠B a = b / SinB; c = bCotB C = 90 - B
If b & ∠C a = b / CosC; c = btanC B = 90 - C
If c & ∠B a = c / CosB; b = ctanB C = 90 - B
If c & ∠C a = c / SinC; b = cCotC B = 90 - C
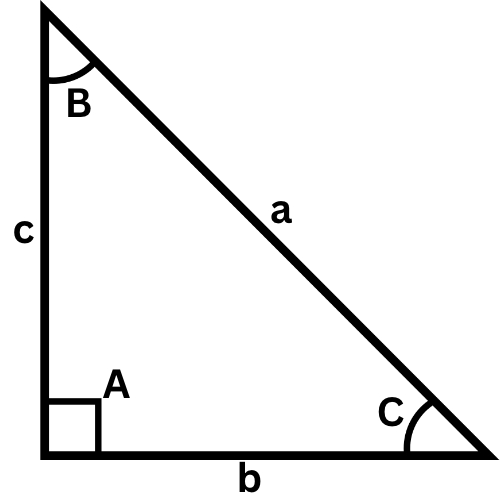
Example: If a is 5, b is 3 then find c, B and C.
Answer: c = √a2 - b2, c = √52 - 32,
c = 4
SinB = b / a,
SinB = 3 / 5,
B = Sin-1(.6),
B = 36.87
C = 90 - B,
C = 90 - 36.87,
C = 53.13
c = 4,
B = 36.87°,
C = 53.13°
