Circles inside a circle, rectangle Calculator
Circles inside a circle:
D:
d:
n:
(Fill any two fields above)
Pattern A: N = 3n2 + 3n + 1 D = (2n + 1)d
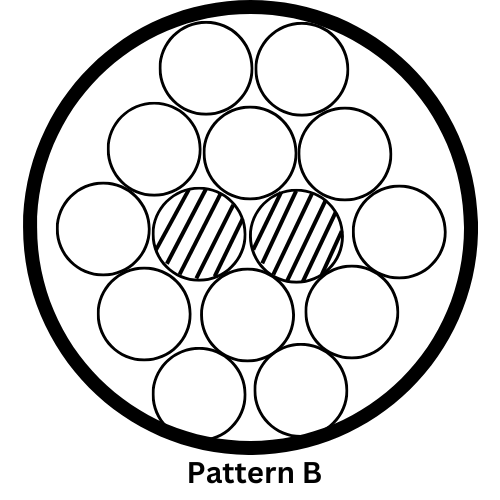
Pattern B: N = 3n2 + 5n + 2 D = (2n + 2)d
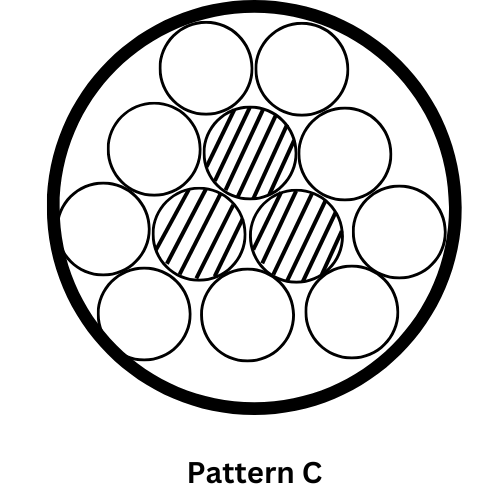
Pattern C: N = 3n2 + 6n + 3 D = (1 + 2 √(n2 + n + 1/3))d
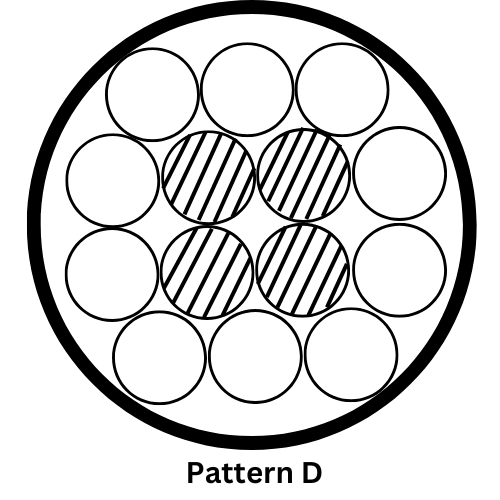
Pattern D: N = 3n2 + 7n + 4 D = (1 + √(4n2 + 5.644n + 2))d
D: Diameter of the enclosing (outer) circle
d: Diameter of the enclosed (inner) circles
n: Number of complete layers over core circle
N: Number of enclosed circles
If N > 10000:
N:
D = d * (1 + √(N/0.907))
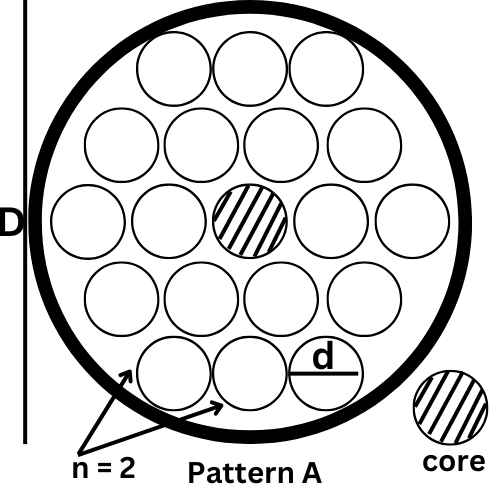
Example: What would be the diameter of the enclosing layer to enclose 19 cables inside it. If each cable has a diameter of 2 cm?
Answer: N = 19, d = 2, D = ?n for N = 19 would be 2 (Pattern A) or you can calculate using N = 3n2 + 3n + 1, 19 = 3n2 + 3n + 1, 18 = 3n2 + 3n, 6 = n2 + n n2 + n - 6 = 0, now use quadratic equation ax2 + bx + c = 0 formula x = (-b ± √(b2 - 4ac)) / 2a to calculate n
n = -1 ± √(12 - 4 * 1 * (-6)) / 2 * 1, n = (-1 + 5) / 2, n = 2
Now we have n = 2, d = 2, D = ? calculate D (Pattern A) D = (2n + 1)d D = (2*2+1)*2, D = 10
Circles inside a rectangle:
r:
c:
d:
A:
(Fill any three fields above)
If H = 0:
Pattern A: V = A = rd * cd
Pattern B: V = A = cd2 * [1 + 0.866 (r - 1)]
r: Number of rows
c: Number of columns
d: Diameter of a circle
V: Total Volume
A: Total Area
H: Height of cylindrical object(s)
If H > 0:
H:
Pattern A: V = A * H
Pattern B: V = A * H
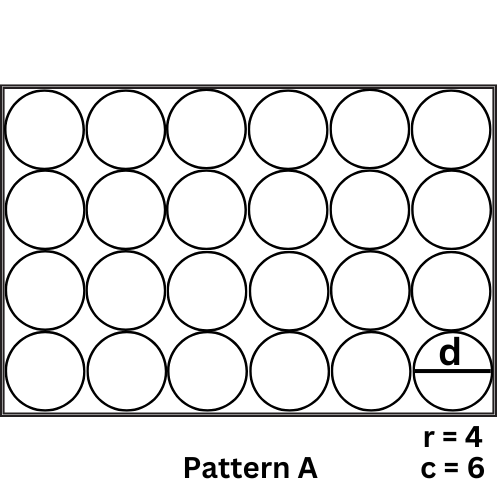
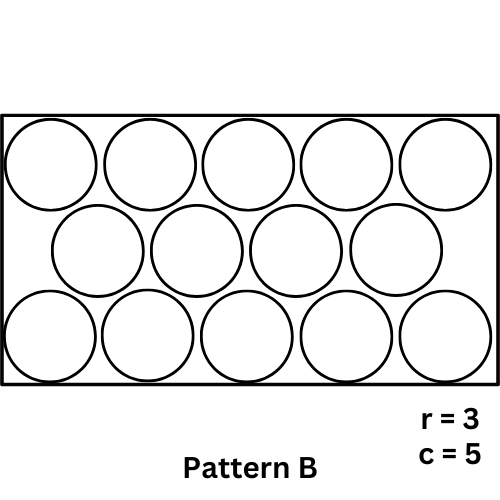
Example: What would be the best way to pack 15 bottles inside a carton. If each having a diameter of 2 cm and height of 10 cm?
Answer: N = 15, d = 2, H = 10, A = ?, V = ?
For N = 15 , r and c can be (3,5) (5,3) (Pattern A)
(2,8) (8,2) (Pattern B)
if r,c (3,5) then A = 60, V = 600 (Pattern A) and A = 54.64, V = 546.4 (Pattern B)
if r,c (2,8) then A = 64, V = 640 (Pattern A) and A = 59.712, V = 597.12 (Pattern B)
In both cases Pattern B shows less area and volume to pack the bottles.
